Экономическая задача ориентирована на реальную жизнь. В этих заданиях
рассматриваются идеализированные жизненные ситуации, которые являются
некоторыми текстовыми упрощениями, моделями, реально возникающих, например,
при обращении в банк, покупке или продаже ценных бумаг, выпуске производственной
продукции и получении прибыли.
Целью курса является обучение векторно – координатному методу решения задач школьного курса геометрии
Статистическая грамотность — неотъемлемая часть экономическо-го образования, а статистическая информация — важнейший ресурс управления. «Знание статистики подобно знанию иностранных язы-ков или алгебры: оно может пригодиться в любое время и при любых обстоятельствах», — считал английский статистик А. Боули.
Для хорошей подготовки к экзамену необходимо целенаправленное повторение разделов курса алгебры и геометрии.
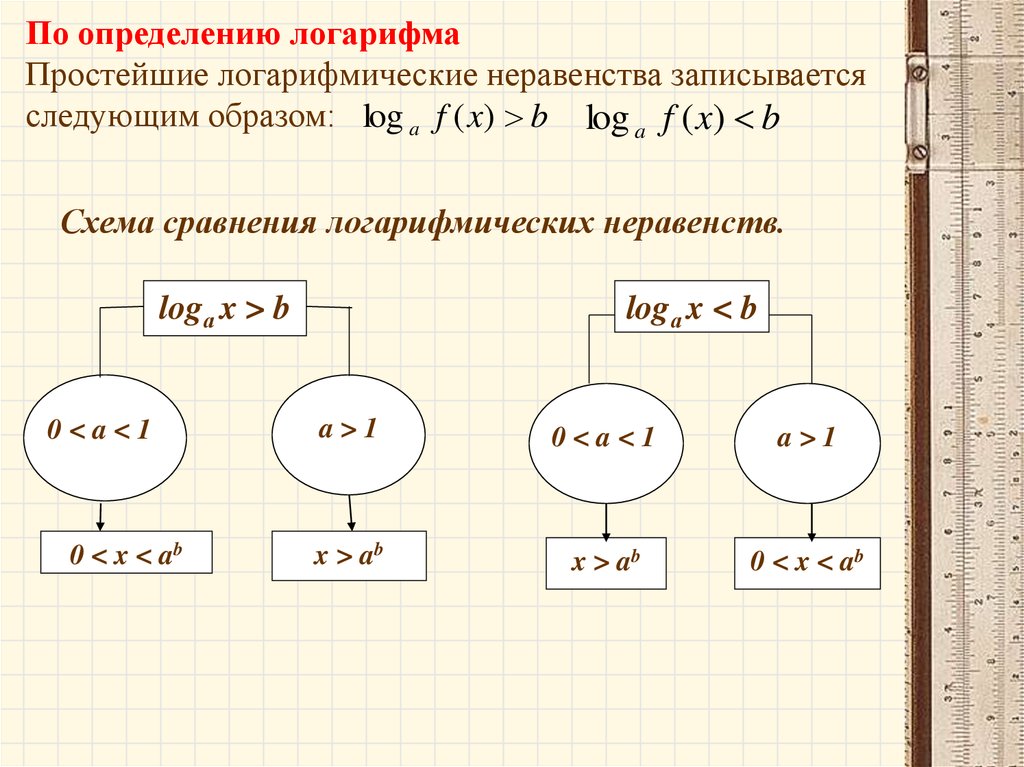
Логарифмическим неравенством называется неравенство, содержащее
переменную под знаком логарифма и/или в основании логарифма.
Логарифмические неравенства, как и показательные неравенства, в общем случае не решаются в виде формул (аналитически). Их можно решать
только приближенно численными методами на компьютерах. А вот экзаменационные задачи специально составлены так, что их можно решить аналитически. Иными словами, Вы можете (и должны!) проделать такие тождественные преобразования, которые приводят заданное логарифмическое неравенство к самому простому логарифмическому неравенству. Это самое
простое неравенство так и называется простейшим логарифмическим неравенством. А вот простейшее логарифмическое неравенство решается в самом
общем виде.
Из этих общих рассуждений следуют вполне конкретные рекомендации. Для успешного решения логарифмических неравенств необходимо:
- Четко решать простейшее логарифмическое неравенство.
- Не только знать все логарифмические тождества, но и множества
значений переменной, на которых эти тождества определены, чтобы
при использовании этих тождеств не приобретать лишних решений,
а тем более, - не терять решений неравенства.
Подробно и без ошибок проделывать математические преобразования
неравенств. При этом сами выкладки должны делаться автоматически руками, а голова должна думать об общей путеводной нити решения.
1) При b < 0 и b = 0 это уравнение, согласно свойству 1 показательной функции, не имеет решения.
2) При b > 0 используя монотонность функции и теорему о корне, уравнение имеет единственный корень. Для того, чтобы его найти, надо b представить в виде b = aс, аx = bс ó x = c или x = logab.
Показательные уравнения путем алгебраических преобразований приводят к стандартным уравнения, которые решаются, используя следующие методы:
1) метод приведения к одному основанию ;
2) метод оценки;
3) графический метод;
4) метод введения новых переменных;
5) метод разложения на множители;
6) показательно – степенные уравнения;
7) показательные с параметром.
Статистика — самостоятельная общественная наука, имеющая свой предмет и методы исследования, которая возникла из потребностей общественной жизни. Статистика — это наука, изучающая количественную сторону всех социально-экономических явлений. Термин «статистика» происходит от латинского слова «статус», которое обозначает «положение, порядок».
В первый раз его употребил немецкий ученый Г. Ахенваль (1719-1772). Главной задачей статистики является математически правильно описать собранные сведения. Статистику можно назвать специальным разделом математики, которая описывает ту или иную сторону жизнедеятельности человека. Статистика использует самые различные математические мегоды и приемы, чтобы человек мог проанализировать ту или иную проблему.
Тригономе́трия (от греч. τρίγονο (треугольник) и греч. μετρειν (измерять), то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии[1]. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре. Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография
